Technology and Math: increasing student learning
- By Ms. Mariana Pires

- May 11, 2018
- 6 min read
Updated: May 14, 2018
Since the start of my career in teaching some 9 years ago, I have always been interested in educational technology. After a couple of years in the classroom, I had an extremely challenging class. I struggled daily to get through lessons without a major meltdown or loud interruptions. More and more I started relying on technology. I would have students listen to reading, work on math problems, and play educational games. The class would work quietly, I would breathe a sigh of relief, and pat myself on the back. You see, I was proud of being a teacher who integrated technology into lessons.
"No doubt, your students were engaged." And then she asked, "but how was that work different from a math worksheet?"
That year, I had a wonderful vice principal who came to observe me. At our debrief she casually mentioned, "No doubt, your students were engaged." And then she asked, "but how was that work different from a math worksheet?" That question stuck with me. She was right to ask. That particular assignment was not any better than a worksheet. I was simply swapping paper and pen for technology. I knew then I needed to elevate my craft.
The problem is, simply adding technological tools does not seem to have an inherent benefit to student achievement. In general, as educators, we are failing to prepare U.S. students to be proficient in an increasingly STEM dependent world (Rutherford et al., 2010). So how can we improve students' understanding by using technology? I set out to find out just that during my Master's program.
The Innovation: Lesson Design
I designed a project in which I would compare and contrast two units of elementary math in my 4th grade classroom. In Stage 1, the students would learn multiplication and technology was not integrated. In Stage 2, the students would work on division and technology was integrated. Both units were designed based on Bruner's modes of representation. Bruner, an American psychologist who made significant contributions to educational psychology, wrote several books about education. He believed that education should not solely rely on memorization. Was he the grandfather of Common Core? I can not state that for sure, but I'm also not saying he wasn't!
Bruner suggested the most effective way to introduce a skill was to follow the natural evolution of the thought process (1960). He described how to do so in 3 phases: concrete, iconic, and abstract. I designed the entire lesson for my innovation based on Bruner's modes of representation.
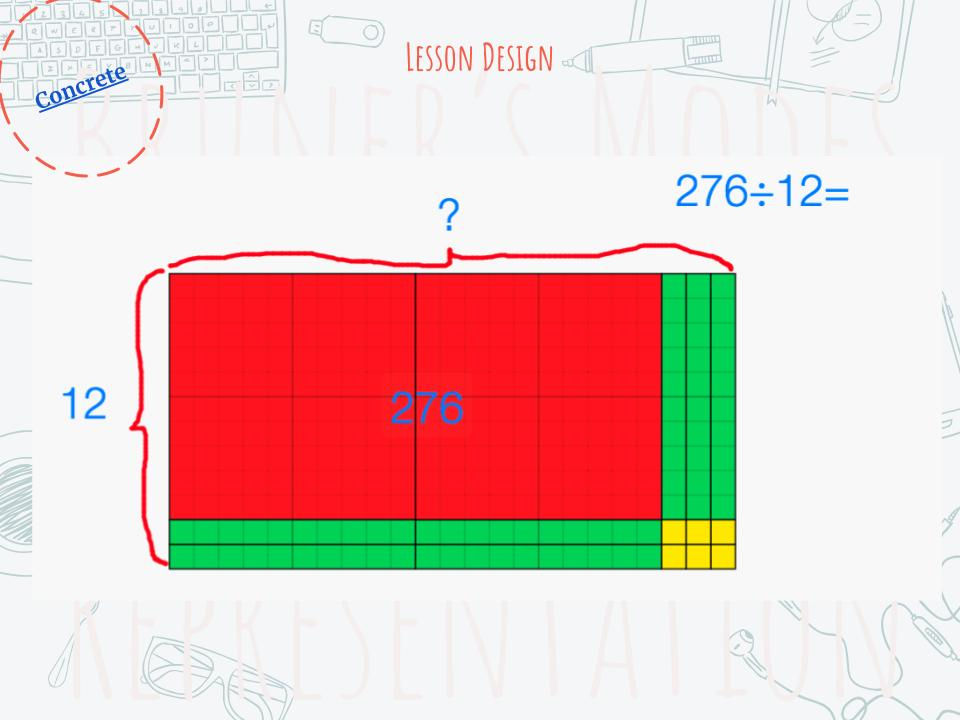
In the concrete phase, students must use materials and have a hands-on approach to building their own knowledge of the skill. Since I chose math for my project, the concrete phase used manipulatives, more specifically, base-ten blocks. In Stage 2, students used their previous knowledge of area model in geometry and multiplication to build them to solve division problems.
Virtual manipulatives were a great way for students to practice. They used the dividend as the area, and length as the divisor. Understanding that the width and the length must be multiplied to get the area of a rectangle, the students were able to discover that given the area and one of the sides, they could discover the other side, in this case the quotient.
The iconic phase is the bridge between the concrete and abstract. It consists of a graphic representation to build upon the knowledge the students have internalized. In my classroom, the students created a modified area model with partial quotients. They started by learning about friendly numbers, which are large multiples of the divisor. Students could then use the friendly numbers to break the large dividend down into smaller mental math problems. Students also wrote a word problem to match their division problem. The word problem provided me with a glance into their understanding of the concept.
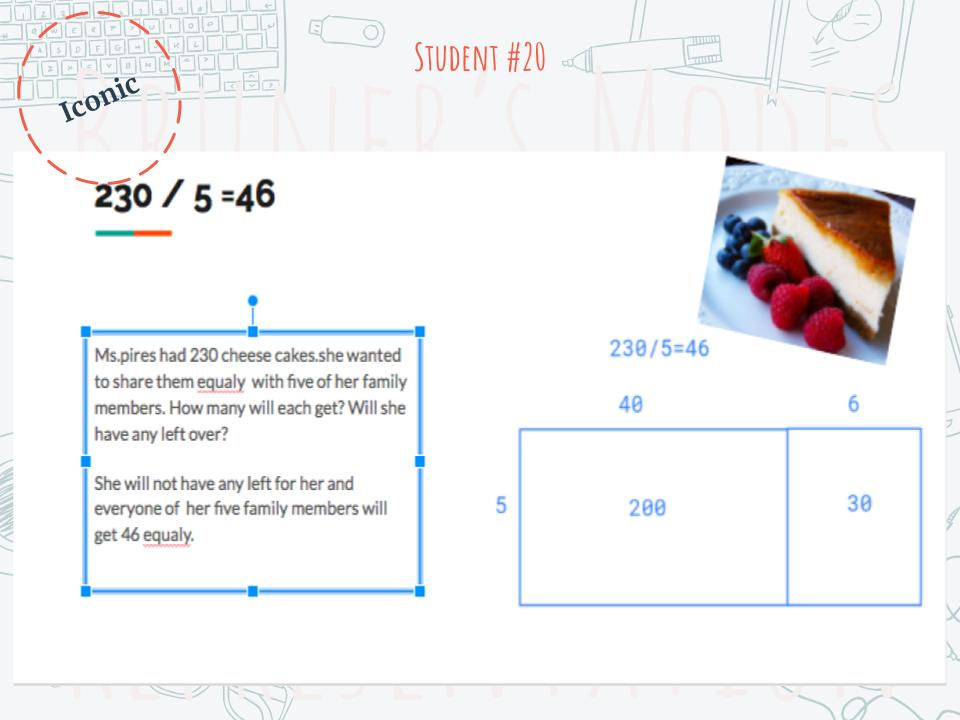
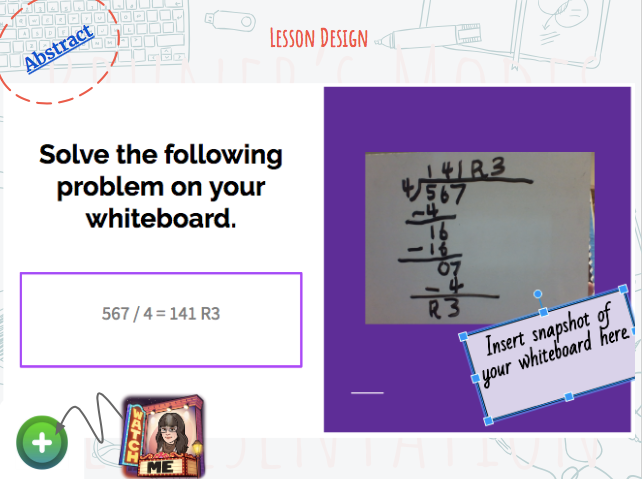
Finally, the abstract phase includes interacting with the skill using only language. In this case, numbers and signs which are considered the language of math. The abstract phase is the long awaited traditional algorithm. By this point, the students were begging for the traditional algorithm which feels, and in fact it is, a shortcut! When my kiddos arrived at this point, they had a deeper understanding of the concept and did not simply memorize the algorithm. Students were able to record a tutorial on FlipGrid on how to use the algorithm.
The data I collected in my project confirmed that the majority of my classroom was able to internalize and explain the concept of long division.
The Findings
In the question of how technology can increase student learning, I found that three conclusions could be asserted.
1) For student learning, the tech tools matter! Not all tech tools are created equal! The simple presence of technology doesn't guarantee students will learn more. The technology educators choose for each lesson makes all the difference. Lee Shulman, a Stanford professor and famous educational theorist, described in one of his books that best teaching practices must include pedagogy knowledge and content knowledge. This was called PCK, pedagogy content knowledge (1987). In the last few years, other theorists have added technology into Shulman's framework, calling it now TPACK. The new framework suggests that teachers must use technology in a way that combines "their knowledge of what makes concepts difficult or easy to learn and how technology can help redress some of the problems that students face" (Koehler et al., 2013, p.16). Ask yourself, can this be done as easily without technology? If the answer is yes, then you might not be allowing the technology to be used to its full potential.
Teachers must use technology in a way that combines "their knowledge of what makes concepts difficult or easy to learn and how technology can help redress some of the problems that students face" (Koehler et al., 2013, p.16).
Tech tools must provide the ability for students to:
share their knowledge in new and creative manners
share their work with an authentic audience
explore their work through innovative and user-friendly tools
2) Tech must be used in a way to create higher level thinking! As former Secretary of Education Richard Riley memorably put it, "We are currently preparing students for jobs that don't yet exist, using technologies that haven't been invented, in order to solve problems that we don't even know are problems yet" (Riley, as quoted in Crutcher, 2007, pp. 18 - 19). The biggest gift we can give our students is to teach them to think outside of the box. To foster higher level thinking, students must understand the underlying concepts being presented.
"We are currently preparing students for jobs that don't yet exist, using the chnologies that haven't been invented, in order to solve problems that we don't even know are problems yet"

Students seem to have more buy in, be more motivated, and be more focused when technology is being utilized. For example, during Stage 1, when requested to explain in writing how the student used the traditional algorithm to solve the problem, student #1 wrote exactly 10 words. The same student, when given the option to record the answer, spoke for 1 minute and 7 seconds. Here is a small portion of what was said in the recording. As one can see, the student seemed more invested during Stage 2, and therefore explained the concepts in a much deeper manner while using math vocabulary.
Higher level thinking is fostered by technology when:
students are able to demonstrate their thinking better
students are more focused and motivated
students have more buy in
students feel more prepared for the subsequent skills
3) Technology reaches its full promise with struggling students! Have you been wondering how to reach one of your struggling students? Technology just might be the answer. During my project, the data in favor of technology was the most compelling for my struggling group of students. This group made a growth of 17% during Stage 2, whereas the same group made a growth of only 5% without technology. Why such a huge difference? Technology in the classroom "grabs attention because it offers novelty and variety compared to lessons taught in a traditional manner" (Dietrich & Balli, 2014, p. 27).
Technology helps struggling students because:
novelty and variety serve as a hook
students may move at their own pace
students may be given the chance to answer questions verbally rather than in writing
students received feedback faster
The question for educators is not if we should use technology but how we are using it to make the largest impact in math comprehension and in education in general!
My lessons for each phase of Bruner's modes of representation are linked to the photos below. Please feel free to use them!


Comments